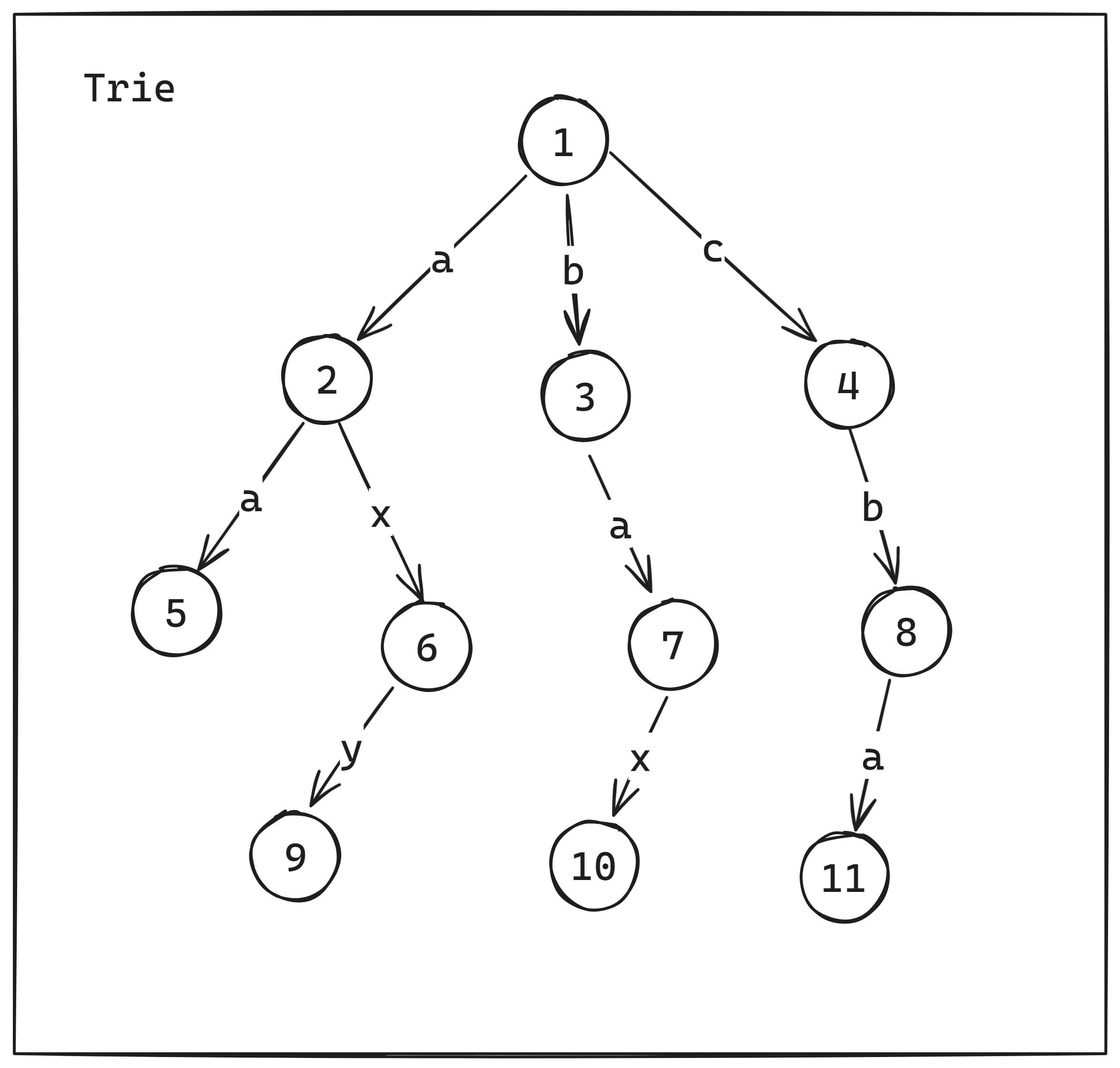
字典树
声明:以下介绍均基于本人理解
概述
- 字典树(Trie),像字典一样的树
属性
- 树:一棵有根的树
- 结点:一般以类似键值对的形式存在,即包含两个成员信息:字符(key)作为结点标识,数值(value)作为标识出现的频率
- 应用:检索字符串(例如字符串本身或其前缀、后缀等)
模板
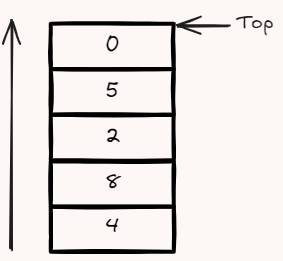
数组结构存储
数组结构示例图
代码(数组树)
1 |
|
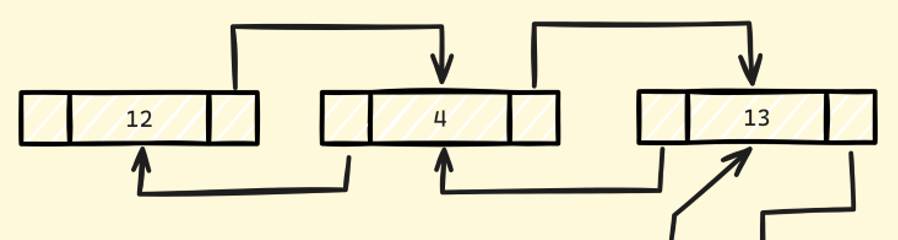
链表结构存储
结点结构示例图
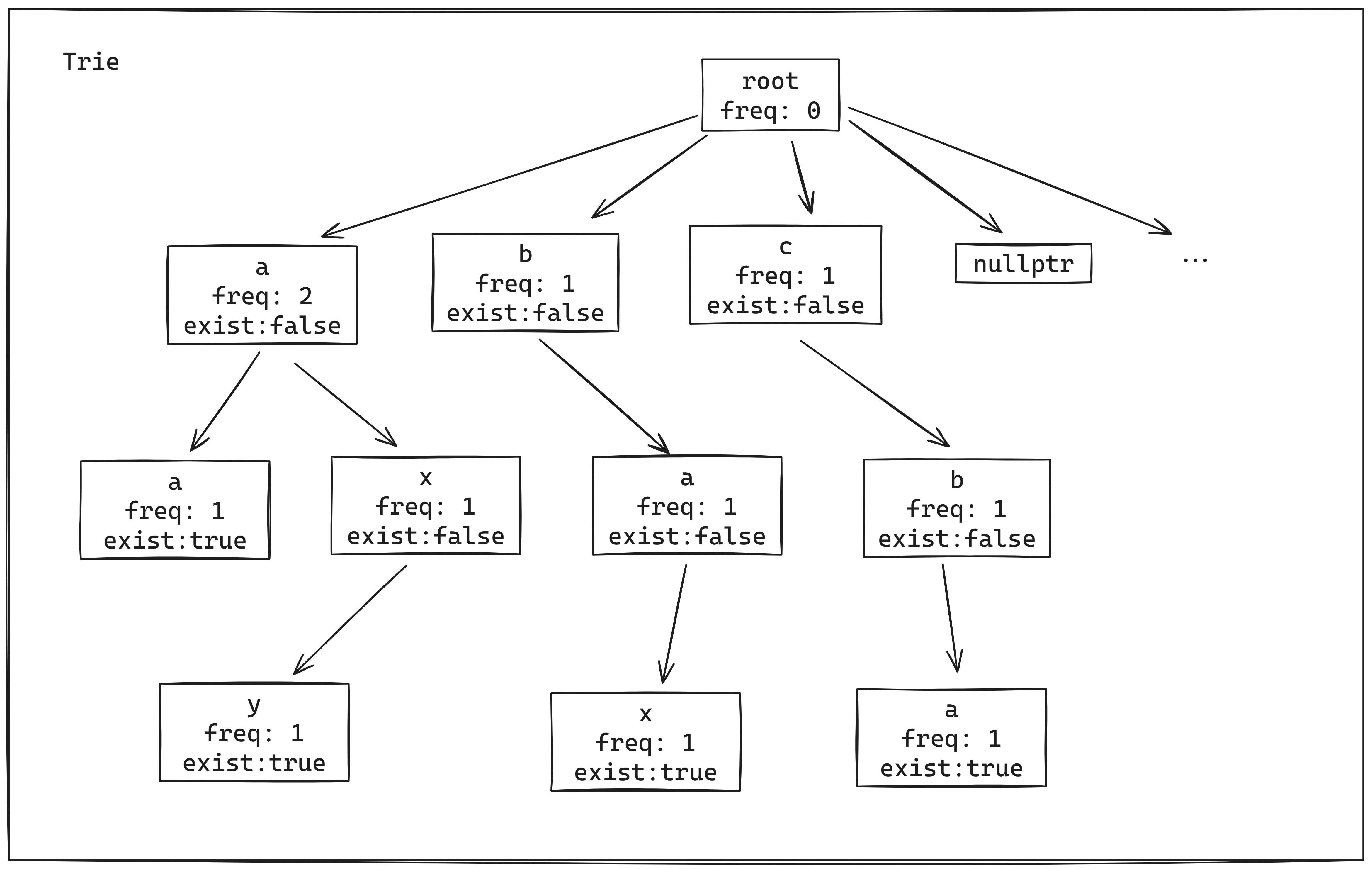
代码(链表树)
1 |
|
复杂度分析
预设所有字符串总长度为n
- 构造字典树
- 空间: O(nK)(对于结构体而言K为结点大小,对于数组而言K = 26)
- 时间: O(n)
- 检索
- 时间:O(n)
题单
参考来源:灵茶山艾府
- [x] 208 实现 Trie (前缀树)
- [x] 2416 字符串的前缀分数和
- [ ] 336 回文对
- [ ] 745 前缀和后缀搜索
- [ ] 3045 统计前后缀下标对 II
- [x] 3093 最长公共后缀查询
发散/随想/自身理解(?)
- 字典树突出有序匹配,对前后缀有特效
- 应用方面,以结构体示例,若标识不限字符,那么检索的目标即从字符串扩展到某种序列。
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Forgotten Area!