简介

  • 此文是对 运算器 章节的知识补充，主要涉及到逻辑代数的运算。内容不全面，此文未详细提及的其它知识请自行补充
  • 逻辑代数运算主要用于分析和设计数字电路，代数的变量值有两种，1 和 0 (在数理逻辑中被称为 真 和 假)，主要包含 与 , 或 , 非 三种基本逻辑运算，此外还有与非，或非，与或非，异或等运算

相关运算符号说明

所展示的部分符号不一定用于代数运算中，列举出来想表达的是部分符号具有相同/相似的效果

运算符号

与

  • 表示符号
    • ⋅\cdot (点乘)(主要用于代数运算，可省略)
    • ∩\cap (交集)(集合论，表示两个集合的交集)
    • ∧\land (合取)(数理逻辑中表示"与"的命题联结词)
    • &\& (按位与), &&\&\& (逻辑与)(这两个符号在计算机编程语言中较为常见)
  • 逻辑表达式:

Y=A⋅B=ABY = A \cdot B = AB

  • 真值表
A B Y
0 0 0
0 1 0
1 0 0
1 1 1

或

  • 表示符号
    • ++ (加号)(主要用于代数运算)
    • ∪\cup (并集)(集合论，表示两个集合的并集)
    • ∨\lor (析取)(数理逻辑中表示"或"的命题联结词)
    • ∣| (按位或), ∣∣|| (逻辑或)(这两个符号在计算机编程语言中较为常见)
  • 逻辑表达式:

Y=A+BY = A + B

  • 真值表
A B Y
0 0 0
0 1 1
1 0 1
1 1 1

非

  • 表示符号
    • A‾\overline{A} (上划线), ′'(单引号)(主要用于代数运算)
    • ∁UA\complement_{U}A (补集)(集合论，表示在全集 UU 内 AA 的补集)(有点类似非的概念)
    • ¬\lnot (非)(数理逻辑中表示"非"的命题联结词)
    •  ~ (按位非), !! (逻辑非)(这两个符号在计算机编程语言中较为常见)
  • 逻辑表达式:

Y=A‾Y = \overline{A}

  • 真值表
A Y
0 1
1 0

与非

  • 表示符号
    • 在代数运算中是 与 符和 非 符的组合，例如 A⋅B‾=AB‾\overline{A \cdot B} = \overline{AB}
    • ↑\uparrow (数理逻辑中表示"与非")
  • 逻辑表达式:

Y=AB‾Y = \overline{AB}

  • 真值表
A B Y
0 0 1
0 1 1
1 0 1
1 1 0

或非

  • 表示符号
    • 在代数运算中是 或 符和 非 符的组合，例如 A+B‾\overline{A + B}
    • ↓\downarrow (数理逻辑中表示"或非")
  • 逻辑表达式:

Y=A+B‾Y = \overline{A + B}

  • 真值表
A B Y
0 0 1
0 1 0
1 0 0
1 1 0

异或

  • 表示符号
    • 在代数运算中用 与 符，或 符和 非 符表示
    • ⊕\oplus (数理逻辑符号)
    • ^ (计算机编程语言中较常见)
  • 逻辑表达式:

Y=AB‾+A‾BY = A \overline{B} + \overline{A} B

  • 真值表
A B Y
0 0 0
0 1 1
1 0 1
1 1 0

同或

  • 表示符号
    • 在代数运算中用 与 符，或 符和 非 符表示
    • ⊙\odot (数理逻辑符号)
  • 逻辑表达式:

Y=AB+A‾B‾Y = AB + \overline{A} \overline{B}

  • 真值表
A B Y
0 0 0
0 1 1
1 0 1
1 1 0

简单说明

  • 在现实的电子电路中，逻辑运算可以不需要包含上述所有符号，仅需要包含其中几种符号就可以完成所有运算
    1. 从数理逻辑上看，若一个由运算符构成的集合能把其它运算符表示出来，那么该集合是完备的，如果这个完备集已经不能再小了，那么该集合称为最小完备集。(例如 { ∧,¬\land, \lnot }, { ∨,¬\lor, \lnot }, { ↓\downarrow }, { ↑\uparrow } 是最小完备集; { ∧,∨,¬\land, \lor, \lnot } 是完备集; { ∧,∨\land, \lor } 不是完备集，无法表示 ¬\lnot )
    2. 在电路元器件的生产中，由于各个厂商的使用的材料、工艺等可能具有差异，所制作的门电路内部属性(输入、输出延时等)均不同，在使用仿真软件导入库时，原先设计的电路可能被优化，仅使用特定的几种门电路构成整个电路

运算法则

常量与变量间的关系

  • 自等律: A+0=AA + 0 = A, A⋅1=AA \cdot 1 = A
  • 0 - 1律: A+1=1A + 1 = 1, A⋅0=0A \cdot 0 = 0
  • 重叠律: A+A=AA + A = A, A⋅A=AA \cdot A = A
  • 还原律: A‾‾=A\overline{\overline{A}} = A
  • 互补律: A+A‾=1A + \overline{A} = 1, A⋅A‾=0A \cdot \overline{A} = 0

逻辑代数基本运算法则

  • 交换律:
    • A+B=B+AA + B = B + A
    • A⋅B=B⋅AA \cdot B = B \cdot A
  • 结合律:
    • (A+B)+C=A+(B+C)(A + B) + C = A + (B + C)
    • (A⋅B)⋅C=A⋅(B⋅C)(A \cdot B) \cdot C = A \cdot (B \cdot C)
  • 分配律:
    • A⋅(B+C)=A⋅B+A⋅CA \cdot (B + C) = A \cdot B + A \cdot C
    • A+(B⋅C)=(A+B)⋅(A+C)A + (B \cdot C) = (A + B) \cdot (A + C)
  • 反演律:
    • A+B‾=A‾⋅B‾\overline{A + B} =\overline{A} \cdot \overline{B}
    • A⋅B‾=A‾+B‾\overline{A \cdot B} =\overline{A} + \overline{B}
  • 吸收律:
    • A+AB=AA + AB = A
    • A(A+B)=AA(A + B) = A
  • 对偶关系: 将某个逻辑表达式的与和或符号交换，得到一个新的逻辑表达式，为原逻辑式的对偶式，若原逻辑恒等式成立，则对偶式也成立(例如吸收律的两个表达式)

逻辑函数表示方法

  1. 列逻辑状态表(真值表)
  2. 逻辑式(例: Y=ABY = AB)
  3. 逻辑(电路)图
  4. 卡诺图

卡诺图

  • 变量的最小项对应的按一定规则排列的方格图，每个方格代表一个最小项
    例: Y=A‾+A‾B‾+BCD+BD‾Y = \overline{A} + \overline{A}\overline{B} + BCD + B\overline{D}, 卡诺图如下:
    卡诺图
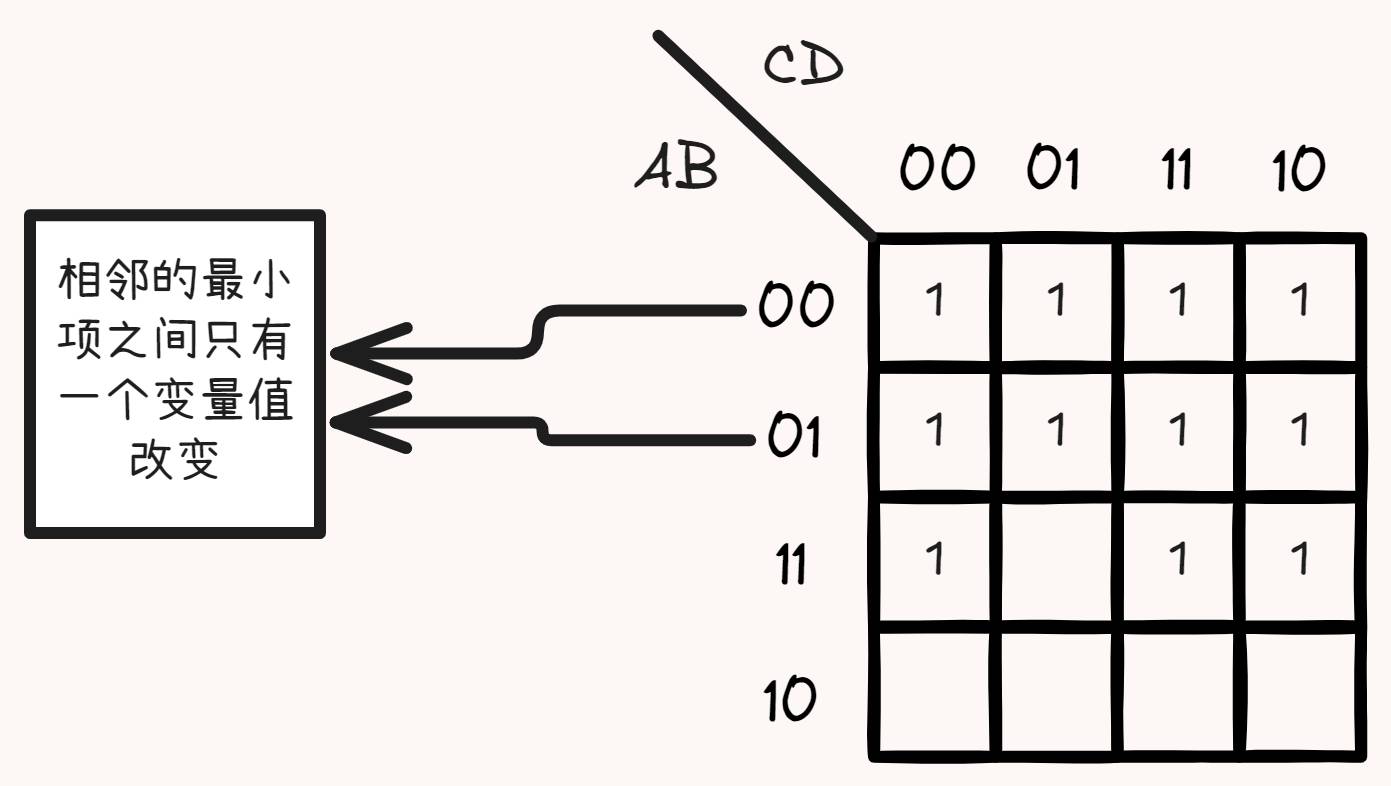
  • 化简
    • 取值为1的相邻最小项画圈，个数必须为 2n,(n=0,1,2...)2^{n}, (n = 0, 1, 2...)
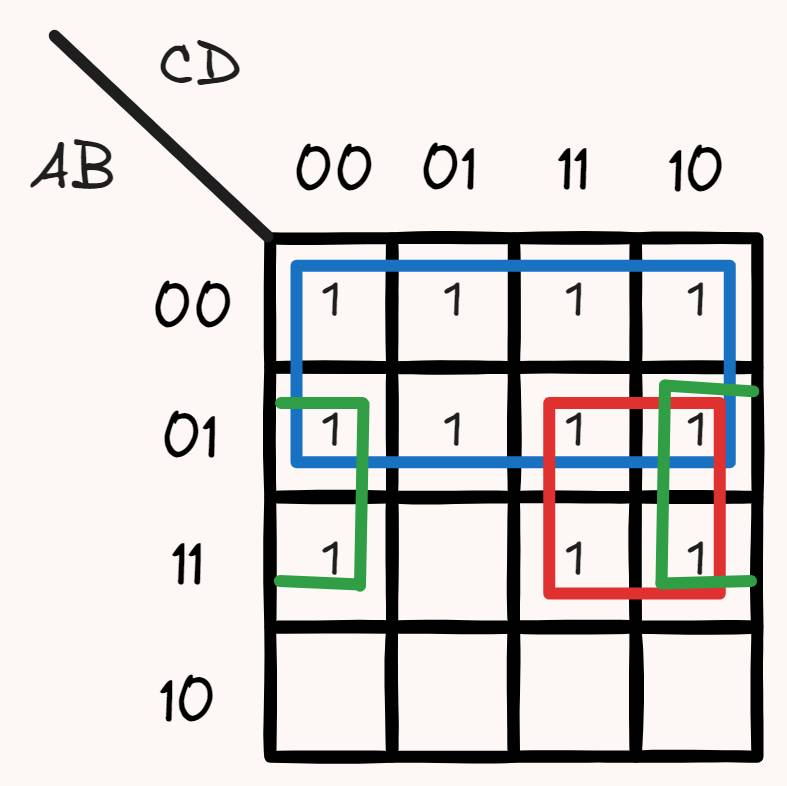
      卡诺图化简
    • 合并最小项
      • 蓝圈表示 A‾\overline{A}
      • 红圈表示 BCBC
      • 绿圈表示 BD‾B\overline{D}
    • 最终化简的结果是 Y=A‾+BC+BD‾Y = \overline{A} + BC + B\overline{D}