简要

参考资料：《深度学习》（花书）。
此模板仅作知识的查漏补缺，因此不作全面具体介绍。

矩阵相关

矩阵转置

(A⊤)i,j=Aj,i\begin{aligned} (\boldsymbol{A}^\top)_{i,j} = A_{j,i} \end{aligned}

  • 标量的转置等于它本身。

单位矩阵和逆矩阵

单位矩阵：In(In∈Rn∗n)\boldsymbol{I}_n(\boldsymbol{I}_n \in \mathbb{R}^{n*n})

∀x∈Rn,Inx=x\begin{aligned} \forall\boldsymbol{x} \in \mathbb{R}^{n},\boldsymbol{I}_n\boldsymbol{x}=\boldsymbol{x} \end{aligned}

矩阵 A\boldsymbol{A} 的矩阵逆记作 A−1\boldsymbol{A}^{-1} ，其定义的矩阵满足如下条件：

A−1A=In\begin{aligned} \boldsymbol{A}^{-1}\boldsymbol{A}=\boldsymbol{I}_n \end{aligned}

可通过下式求解（当逆矩阵存在时）：

Ax=b\begin{aligned} \boldsymbol{Ax}=\boldsymbol{b} \end{aligned}

A−1Ax=A−1b\begin{aligned} \boldsymbol{A}^{-1}\boldsymbol{Ax}=\boldsymbol{A^{-1}b} \end{aligned}

Inx=A−1b\begin{aligned} \boldsymbol{I_nx}=\boldsymbol{A^{-1}b} \end{aligned}

x=A−1b\begin{aligned} \boldsymbol{x}=\boldsymbol{A^{-1}b} \end{aligned}

线性相关和生成子空间

若 x\boldsymbol{x} 和 y\boldsymbol{y} 都是某方程组的解，则

z=αx+(1−α)y\begin{aligned} \boldsymbol{z} = \alpha\boldsymbol{x} + (1 - \alpha)\boldsymbol{y} \end{aligned}

也是该方程组的解（ α\alpha 取任意实数）

为分析方程 Ax=b\boldsymbol{Ax}=\boldsymbol{b} 有多少个解，可以将 A\boldsymbol{A} 的列向量看作是从原点（元素为0的向量）出发的不同方向，确定有多少种方法可以到达向量 b\boldsymbol{b} 。此时，向量 x\boldsymbol{x} 中的每个元素表示我们应该沿着这些方向走多远，即 xix_i 表示需要沿着第i个向量的方向走多远

Ax=∑ixiA:,i\begin{aligned} \boldsymbol{Ax} = \sum_ix_i\boldsymbol{A}_{:,i} \end{aligned}

这种操作被称为 线性组合。

形式上，一组向量的线性组合，是指每个向量乘以对应标量系数之后的和。

∑iciv(i)\begin{aligned} \sum_ic_i\boldsymbol{v}^{(i)} \end{aligned}

生成子空间： 原始向量线性组合后所能抵达的点的集合

假设有一个 R2∗2\mathbb{R}^{2*2} 的矩阵，两个列向量相同，列向量冗余，其列空间为一条线，不能覆盖整个 R2\mathbb{R}^{2} 空间。

这种冗余被称为 线性相关。

范数

范数： 衡量向量大小的函数，定义如下，其中 p∈R,p≥1p \in \mathbb{R},p\ge1 。

∥x∥p=(∑i∣x∣p)1p\begin{aligned} \left\|\boldsymbol{x}\right\|_p=(\sum_i{\left|\boldsymbol{x}\right|}^p)^{\frac{1}{p}} \end{aligned}

特殊类型的矩阵和向量

对角矩阵： 只在主对角线上含有非零元素的矩阵。 i≠j,Di,j=0i \ne j,D_{i,j}=0

对称矩阵： 转置和自己相等的矩阵。 A=A⊤\boldsymbol{A}=\boldsymbol{A}^\top

单位向量： 具有 单位范数 的向量。 ∥x∥2=1\left\|\boldsymbol{x}\right\|_2=1

若 x⊤y=0\boldsymbol{x^\top y}=0，那么向量 x\boldsymbol{x} 和 y\boldsymbol{y} 互相 正交。如果两个向量都有非零范数，那么这两个向量之间的夹角是90度。在 Rn\mathbb{R}^n 中，至多有 nn 个范数非零向量互相正交。如果这些向量不仅互相正交，并且范数都为1，那么称它们为标准正交。

正交矩阵： 行向量和列向量是分别标准正交的矩阵。 A⊤A=AA⊤=I\boldsymbol{A}^\top\boldsymbol{A}=\boldsymbol{A}\boldsymbol{A}^\top=\boldsymbol{I}， A−1=A⊤\boldsymbol{A}^{-1}=\boldsymbol{A}^\top

特征分解

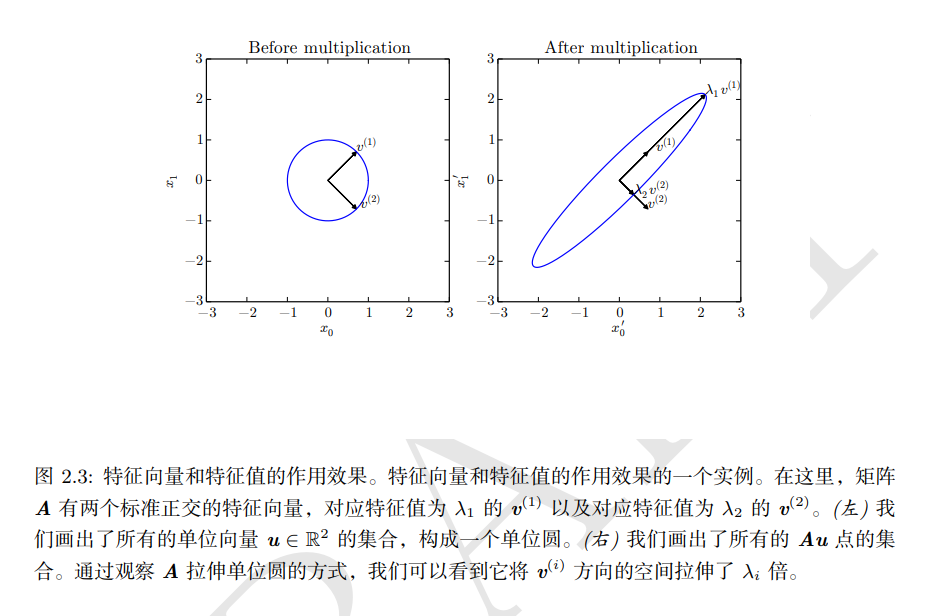
特征分解： 将矩阵分解成一组特征向量和特征值。

方阵 A\boldsymbol{A} 的特征向量是指与 A\boldsymbol{A} 相乘后相当于对该向量进行缩放的非零向量 v\boldsymbol{v}：

Av=λv\begin{aligned} \boldsymbol{Av}=\lambda\boldsymbol{v} \end{aligned}

标量 λ\lambda 被称为这个特征向量对应的 特征值。（类似地，我们也可以定义 左特征向量 v⊤A=λv⊤\boldsymbol{v^\top A}=\lambda\boldsymbol{v^\top}，但是通常更关注 右特征向量）。

如果 v\boldsymbol{v} 是 A\boldsymbol{A} 的特征向量，那么任何缩放后的向量 sv(s∈R,s≠0)s\boldsymbol{v}(s \in \mathbb{R},s\ne 0) 也是 A\boldsymbol{A} 的特征向量。此外，svs\boldsymbol{v} 和 v\boldsymbol{v} 有相同的特征值。基于此原因，通常只考虑单位特征向量。

假设矩阵 A\boldsymbol{A} 有 nn 个线性无关的特征向量 {v(1),…,v(n)}\{\boldsymbol{v}^{(1)},\dots,\boldsymbol{v}^{(n)}\}，对应着特征值 {λ1,…,λn}\{ λ_{1}, \dots,λ_{n}\} 。将特征向量连接成一个矩阵，使得每一列是一个特征向量：V=[v(1),…,v(n)]\boldsymbol{V}=[\boldsymbol{v}^{(1)},\dots,\boldsymbol{v}^{(n)}]，类似地，可以将特征值连成一个向量 λ=[λ1,…,λn]⊤\boldsymbol{λ}=[ λ_{1},\dots, λ_{n}]^\top。因此 A\boldsymbol{A} 的 特征分解 可以记作

A=Vdiag(λ)V−1\begin{aligned} \boldsymbol{A}=\boldsymbol{V}diag(\boldsymbol{\lambda})\boldsymbol{V^{-1}} \end{aligned}

  • 不是每一个矩阵都可以分解成特征值和特征向量。
  • 每个实对称矩阵都可以分解成实特征向量和实特征值：

A=QΛQ⊤\begin{aligned} \boldsymbol{A}=\boldsymbol{Q\Lambda Q^\top} \end{aligned}

其中 Q\boldsymbol{Q} 是 A\boldsymbol{A} 的特征向量组成的正交矩阵， Λ\boldsymbol{\Lambda} 是对角矩阵。特征值 Λi,i\Lambda_{i,i} 对应的特征向量是矩阵 Q\boldsymbol{Q} 的第 ii 列，记作 Q:,i\boldsymbol{Q}_{:,i}。因为 Q\boldsymbol{Q} 是正交矩阵，可以将 A\boldsymbol{A} 看作是沿方向 v(i)\boldsymbol{v}^{(i)} 延展 λi\lambda_i 倍的空间。

特征向量和特征值的作用效果