概述

队列(queue): 一种类似列表的数据结构，元素访问受限，可从两端操作，行为与现实排队基本一致

简单图示

队列

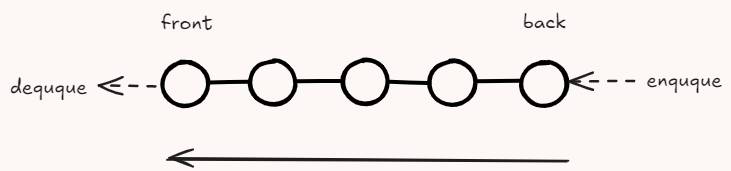
特性

  • 元素从 后端(rear/back) 入队(push/ enqueue), 从 前端(front) 出队(pop/ dequeue)，遵循 先进先出(First In First Out, FIFO) 规则

实现(C++)

ADT

1
2
3
4
5
6
7
8
9
10
class Queue {
public:
    Queue() {}
    virtual ~Queue() {}
    virtual bool enqueue(int data) = 0; // push
    virtual bool dequeue() = 0; // pop
    virtual int front() = 0;
    virtual int rear() = 0;
    virtual int size() { return 0; }
};

链表实现

这个没什么好说的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
struct Node {
    int data;
    Node* next;

    Node(int dat, Node* nxt = nullptr) : data(dat), next(nxt) {}
};

class ListQueue : public Queue {
public:
    ListQueue() : Queue(), virtualHead_(new Node(-1)), tail_(virtualHead_), size_(0) {}
    virtual ~ListQueue() {
        Node* cur = virtualHead_->next;
        while (cur != nullptr) {
            Node* node = cur;
            cur = cur->next;
            --size_;
            delete node;
        }
        delete virtualHead_;
        virtualHead_ = nullptr;
        tail_ = nullptr;
    }
    virtual bool enqueue(int data) override {
        Node* node = new Node(data);
        tail_->next = node;
        tail_ = node;
        ++size_;
        return true;
    }
    virtual bool dequeue() override {
        Node* node = virtualHead_->next;
        if (node == nullptr) return false;
        virtualHead_->next = node->next;
        if (node == tail_) tail_ = virtualHead_;
        delete node;
        --size_;
        return true;
    }
    virtual int front() override {
        Node* node = virtualHead_->next;
        if (node == nullptr) return -1;
        return node->data;
    }
    virtual int rear() override {
        if (tail_ == nullptr) return -1;
        return tail_->data;
    }
    virtual int size() override {
        return size_;
    }

    bool empty() {
        return size_ == 0;
    }

private:
    Node* virtualHead_;
    Node* tail_;
    int size_;
};

数组实现

由于数组是连续存储的，在构造队列的时候，倘若单纯只使用数组存储数据的话，会存在一个问题: 要么入队的操作复杂度是 O(n)，要么出队的复杂度是 O(n)

为解决这个问题，需要构建循环数组来构建队列，使用 取模 方法来实现索引循环操作

使用循环数组构建队列容量是 有限 的，假设支持入队的最大数量为 n，在队列中需要标记前端和后端，分别使用索引 front 和 rear 来指定，一般来说，索引指定的位置能够反映对应的元素值

如果数组大小为 n 的话，会出现一个问题：当 front 和 rear 指向同个位置时，这时候是 不知道 当前队列是满的还是空的，解决方法有 2 个

  1. 最简单的，搞一个参数来记录当前队列的元素数量或状态(空/满)
  2. 由于队列的元素数量有 0, 1, 2, … , n，合计 n + 1 种可能/状态
    • 假设数组大小为 m，有 A={(rear+n−front+1) mod m,0<=front,rear<=n−1}A = \{(rear + n - front + 1) \bmod m, 0 <= front, rear <= n - 1\}, 根据鸽巢/抽屉原理，需要使得 ∣A∣=m=n+1|A| = m = n + 1, 才能无歧义地表示所有可能的队列的元素数量，最终求得: m = n + 1

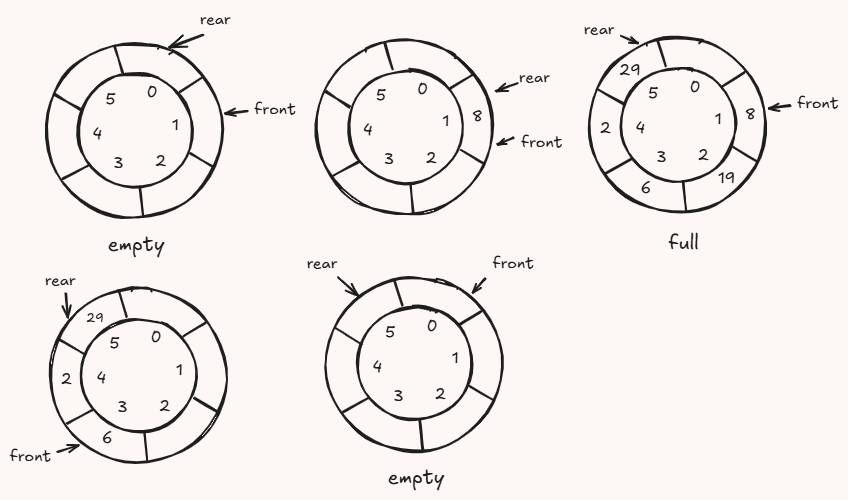
基于循环数组的队列

图中展示的是一个支持元素数量为 m = 5 的循环数组

  • (rear + 1) % m == front 表示空状态
  • (rear + 2) % m == front 表示满状态
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class ArrayQueue : public Queue {
public:
    ArrayQueue() : Queue(), front_(1), rear_(0) {
        memset(datas, 0, sizeof(datas));
    }
    virtual ~ArrayQueue() {
        memset(datas, 0, sizeof(datas));
        front_ = 1;
        rear_ = 0;
    }
    virtual bool enqueue(int data) override {
        if (full()) return false;
        rear_ = (rear_ + 1) % MAX_SIZE;
        datas[rear_] = data;
        return true;
    }
    virtual bool dequeue() override {
        if (empty()) return false;
        front_ = (front_ + 1) % MAX_SIZE;
        return true;
    }
    virtual int front() override {
        if (empty()) return -1;
        return datas[front_];
    }
    virtual int rear() override {
        if (empty()) return -1;
        return datas[rear_];
    }
    virtual int size() override {
        return ((rear_ + MAX_SIZE) - front_ + 1) % MAX_SIZE;
    }

    bool dequeue(int& data) {
        data = front();
        return dequeue();
    }
    bool full() {
        return (rear_ + 2) % MAX_SIZE == front_;
    }
    bool empty() {
        return (rear_ + 1) % MAX_SIZE == front_;
    }

private:
    static const int MAX_SIZE = 101;
    int front_;
    int rear_;
    int datas[MAX_SIZE] = {0};
};

发散/随想/自身理解(?)

  • C++ 中调用 std::queue<>
  • 可以按照某种规则 插队 的队列，一般称为 优先队列
  • 同样的，与其它算法配合打组合拳(例，使用队列作为容器，实现bfs，拓扑排序等等)
  • 队列这个结构用得挺多的，例如 操作系统 的进程调度、消息队列; 软件开发 中搞的任务队列; GUI的事件响应处理队列等等。因为在很多时候，多个任务/事件都需要竞争使用同一资源，或者因为资源制约收到阻塞，队列提供了有序处理的环境，或起到缓冲作用(当然有些任务队列底层有可能是其它的数据结构，例如树(红黑树)等等，看具体情况)
  • 栈和队列本人用的实际不多，不过在刷题的时候，队列可能相对用得多一点; 在工作上看的比较多的就是上一点提到的任务/事件队列，不过好像自己没写过(现在回想一下，遇到的任务队列基本上全是 std::list 搞的，std::queue 真不多，反正最终使用的行为差不多)