运算器

逻辑运算

门电路

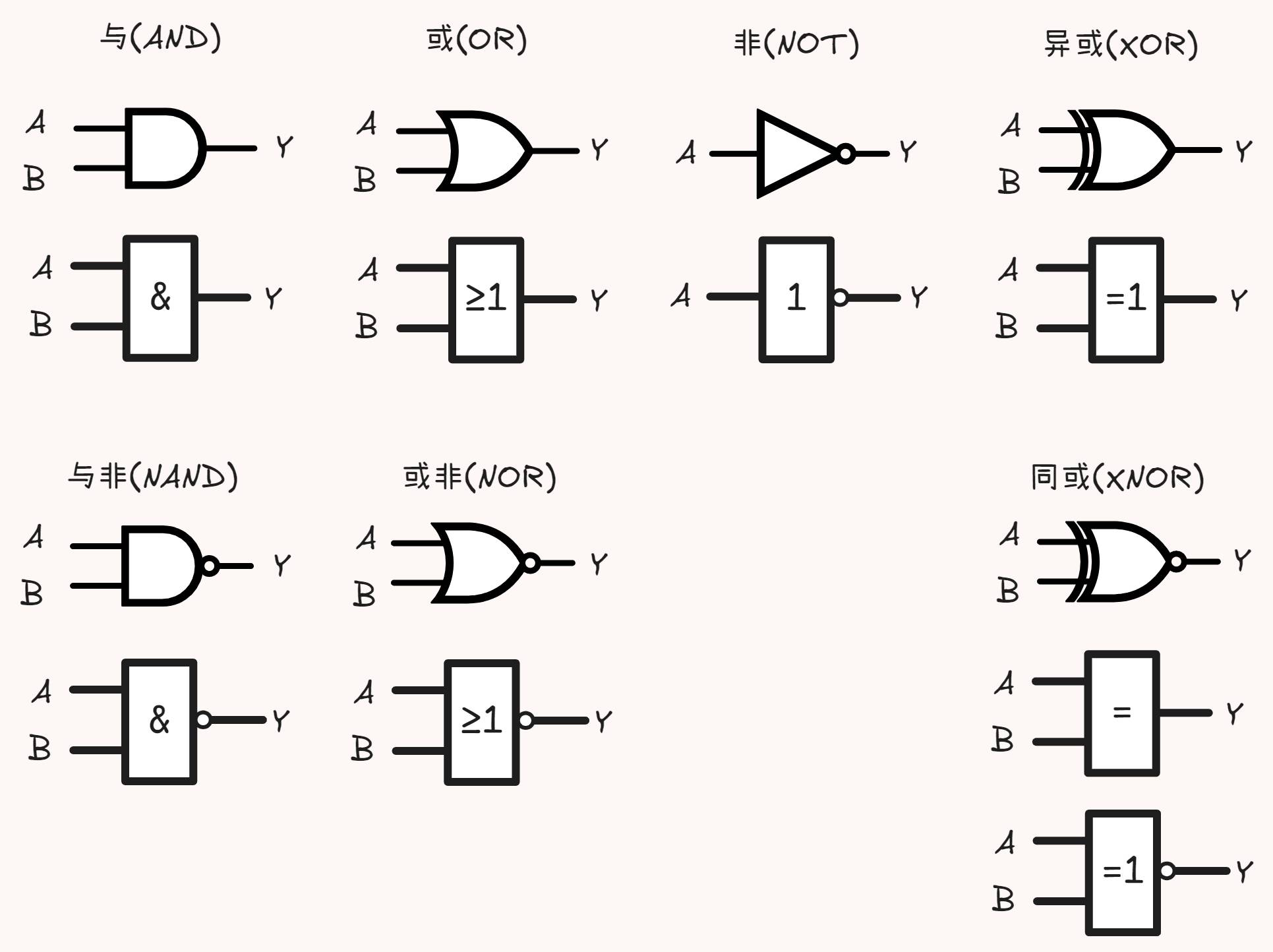
上图展示的是一些较常见门电路，符号上方为常见的表示符号，下方为国标
其中，A 和 B 是输入(实际的门电路输入可能不局限于1到2个，可能更多)，Y 是输出(同输入，可能不止1个输出)

具体表示的逻辑关系运算等知识参考: 逻辑代数运算知识小结

溢出

简述

由于计算机表示的数字大小有限(受 位数 限制)，因此在运算过程中可能出现存储单元无法正确表示超出范围的数字的情况

可能存在的现象

• 对于有符号数而言，可能出现正负数倒转的情况
• 对于无符号数的情况下，可能出现数字重置(清零)/数值由0跳变到最大值的现象

判溢方法

• 单符号位判溢

  • 简述: 正 + 正 = 负(正/上溢); 负 + 负 = 正(负/下溢)
  • 设输入 $A, B$ 的符号位我为 $A_{i}, B_{i}$ ，运算和 $S$ 的符号位为 $S_{i}$
    那么，$V = A_{i} \cdot B_{i} \cdot \overline{S_{i}} + \overline{A_{i}} \cdot \overline{B_{i}} \cdot {S_{i}}$, $V = 1$ 时表示溢出

• 双符号位判溢

  • 正数符号位表示00，负数符号位表示11，当运算结果为01或10时，表示溢出
  • 假设符号位为 $S_{1}S_{0}$ , $S_{1}S_{0} = 01$ 表示正溢，$S_{1}S_{0} = 10$ 表示负溢，$S_{1}$ 表示的始终为正确符号

定点加减法

加法器

• 计算机的定点数以补码的形式表示和存储，加减法均使用加法器做运算($A - B = A + (-B)$)
• 半加器 , 全加器 是两种基础加法器，用于处理一位的加法
• 多位的加法可以由多个全加器组合得到(例如串行加法器由多个全加器连接起来，用于处理多位的加法运算)

半加器

• 半加器不考虑低位进位
• 输入: $A, B$
• 输出: $S$ (和), $C$ (进位)
• 逻辑表达式:
  • $S = A \oplus B$
  • $C = AB$

全加器

• 全加器考虑低位进位
• 输入: $A, B, C_{i-1}$ (第 $i-1$ 位的进位标志)
• 输出: $S_{i}$ (第 $i$ 位和), $C_{i}$ (第 $i$ 位的进位标志)
• 逻辑表达式:
  • $S_{i} = A_{i} \oplus B_{i} \oplus C_{i}$
  • $C_{i} = A_{i}B_{i} + C_{i-1}(A_{i} \oplus B_{i})$

移位

• 移位有左移和右移。从二进制数的形态变化上看，左移/右移即将数每一位往左/右移动一位，从表示的真值上看，每左移/右移一位相当于真值乘/除以2
• 计算机中的移位运算分为三种: 逻辑移位、算术移位、循环移位

逻辑移位

• 将移动的数据视作无符号数
• 左移时最低位补0，其它位的值为其低一位的值
• 右移时最高位补0，其它位的值为其高一位的值

算术移位

• 将移动的数据视作有符号数
• 左移时最低位补0，其它位的值为其低一位的值
• 右移时，最高位(符号位)补符号位的值，其它位的值为其高一位的值

循环移位

• 左移时最高位移入最低位，右移时最低位移入最高位

定点乘除法

乘法

算法

• 手算乘法: 参考乘法竖式运算
• 机器算法：从乘数的最低位开始，每次根据乘数位得到其位积，乘数位为0，位积为0，乘数位为1，则位积为被乘数; 用原部分积右移1位加上本次位积，得新部分积; 初始部分积为0(和手算乘法相似，看似是视角导致差异); 符号位单独异或计算
  1. 列出被乘数和乘数，初始化部分积(运算中间值/最终结果存储的容器)为0
  2. 部分积加上被乘数与乘数末尾的乘积
  3. 部分积、乘数右移1位
  4. 回到步骤2，直到乘数右移至0
• 阵列乘法器，原理类似手算乘法，每个位积的每一位 $x_{i} * y_{i}$ 由一个与门完成，相加使用全加器实现

除法

算法

• 手算除法：参考除法竖式运算
• 原码恢复余数法(类似手算除法，视角有差异)
  • 设 $Q = X / Y$, $R$ 为余数，使用双符号位(符号位不参与运算)
  • X 减去 Y，够减时(R >= 0)该位的商为1, 余数左移1位; 否则为0(R 加回减去的 Y)，余数左移1位。重复操作n次(n应该无具体规定，可以是精度，可以是位数)，最终余数右移n位是余数真正的值
• 原码不恢复余数法
  • 设 $Q = X / Y$, $R$ 为余数，使用双符号位(符号位不参与运算)
  • 加减交替法
    • 余数为正时，商置1，左移，减去 Y
    • 余数为负时，商置0，左移，加上 Y
    • 最后一位商置0时，需要继续恢复余数(最后一位恒置1)
• 补码加减交替法(符号位参与运算的加减交替，总体差异不大)
• 阵列除法器
  • 基本单元: 可控加减单元(CAS)

实现

1. 软件实现
   • 硬件上，没有乘法器和除法器
   • 指令系统上，没有乘除指令，用加减指令和移位指令代替
   • 实现上，乘除法编写子程序实现
   • 算法上， 程序(运行在操作系统上，属于软件层) 中运用串行乘除法计算
   • 运算速度较慢
   • 适用于单片机
2. 硬件乘法器和除法器实现
   • 硬件上，设置有并行加法器、移位器和若干循环、计数控制逻辑电路搭成的串行乘除法器
   • 指令系统上，有乘除指令
   • 实现上，乘除运算通过微程序一级（硬件＋微程序）来实现
   • 算法上， 微程序(直接控制硬件，属于硬件层) 中依据串行乘除运算算法
   • 运算速度有所提高，硬件设计比较复杂
   • 适用于低性能 CPU
3. 高速的阵列乘法器和阵列除法器实现
   • 有专用的、并行运算的阵列乘法器和阵列除法器
   • 指令系统上，有乘除指令
   • 实现上，完全通过硬件实现
   • 算法上，实现并行乘除法
   • 运算速度快，硬件设计相对复杂
   • 适用于高性能 CPU