树基础知识

简要

OI Wiki 树基础
图论中的树和现实生活中的树长得一样，只不过我们习惯于处理问题的时候把树根放到上方来考虑。这种数据结构看起来像是一个倒挂的树，因此得名。

• 与 图论 具有相同目的定位，简单温习离散数学下的树结构
• 在后续的数据结构介绍中，大概率也用不到这么多知识，也存在有些必备知识没有罗列出来的情况，后续在介绍数据章节缺什么就补什么

参考书籍/资料/网站

• Discrete Mathematics (Gary Chartrand, Ping Zhang)
• OI Wiki 树基础

定义

• 树(tree): 无环 的 连通图
  • 一个没有固定根结点的树称为 无根树(unrooted tree)
  • 在无根树基础上，指定一个结点为 根，形成一个 有根树(rooted tree)，有根树一般规定结点之间的 上下级 关系
• 生成树(spanning tree): 一个 连通图 的 生成子图, 同时要求是 树, 即从边集中选择 n - 1 条边连通所有顶点
  • 当一个图是树时，该图只有一个生成树，即它 自身
• 森林(forest): 无环 的 图
  • 森林中每个 连通分量 都是一棵 树
  • 一棵树也可以称为森林

性质/定义扩展

普遍性质

• 图 $G = (V, E) (|V| = n, |E| = m)$, 满足以下 3 个条件中的 2 个时，该图就是树:
  1. G 是连通的
  2. G 是无环的
  3. n = m + 1
• 叶结点(leaf node)
  • 无根树: 度数 不超过 1 的结点
  • 有根树: 没有子结点 的结点

有根树

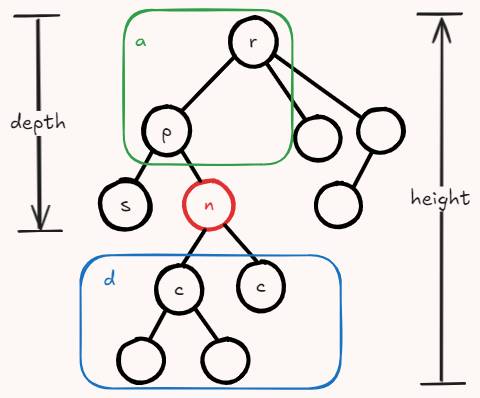
• 根结点 r
• 以结点 n 为主视角:
  • 祖先 a (ancestor): 结点 n 到根结点路径上除 n 本身外的其它结点
  • 父亲结点 p (parent node): 结点 n 到根结点路径上的第二个结点
  • 子结点 c (child node): 以 n 作为父结点的结点
  • 后代 d (descendant): 以 n 作为祖先的结点
  • 兄弟 s (sibling): 同个父结点的多个子结点互为兄弟
  • 结点深度(depth): 结点到根结点路径上的边数(层数由上往下数, 根结点层数为0或1由具体情况而定, 在此将根结点视为深度0, 结点 n 深度为 2)
  • 子树(subtree): 切断结点 n 与父结点相连的边后，该结点所在的子图(结点 n 与其后代构成的树)
• 树的高度(height): 所有结点深度的最大值(层数由下往上数, 根结点层数为0或1由具体情况而定, 在此将根结点视为深度0, 树高为 4)

有根二叉树(rooted binary tree)

• 每个结点最多有两个子结点，子结点顺序通常加以区分，分别为 左子结点 和 右子结点
• 大多数情况下，二叉树指的是有根二叉树

完整二叉树(full/proper binary tree)

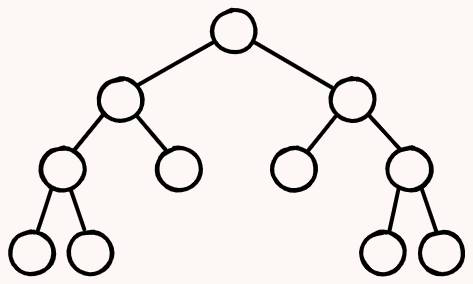
• 每个结点的子结点数量为 0(叶结点)或 2(左右子结点非空)

完全二叉树(complete binary tree)

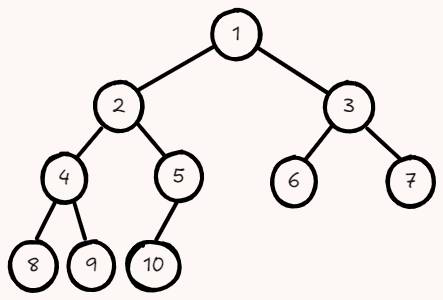
• 只有最下面两层结点的度数可以小于 2，且最下面一层的结点都集中在该层最左边的连续位置上

完美二叉树(perfect binary tree)

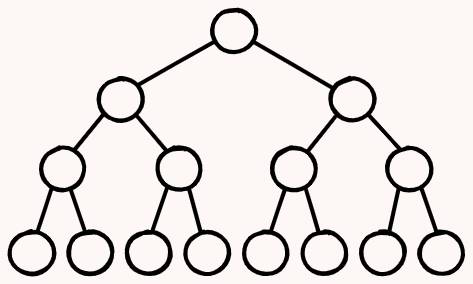
• 所有叶结点的深度均相同，且所有非叶结点的子结点数量均为 2 的二叉树
• 深度为 $k$ 的完美二叉树有 $2^{k} - 1$ 个结点

中文定义与英文定义有所偏差，满二叉树 在此指的是完美二叉树，不是完整二叉树

树遍历

• DFS
• BFS
• 二叉树遍历
  • 先序遍历: 按照 根，左，右 顺序遍历
  • 中序遍历: 按照 左，根，右 顺序遍历
  • 后序遍历: 按照 左，右，根 顺序遍历