数据结构与算法简述
简介
在计算机科学中,数 是核心概念,使用计算机的过程实际上就是对数做各种各样的操作
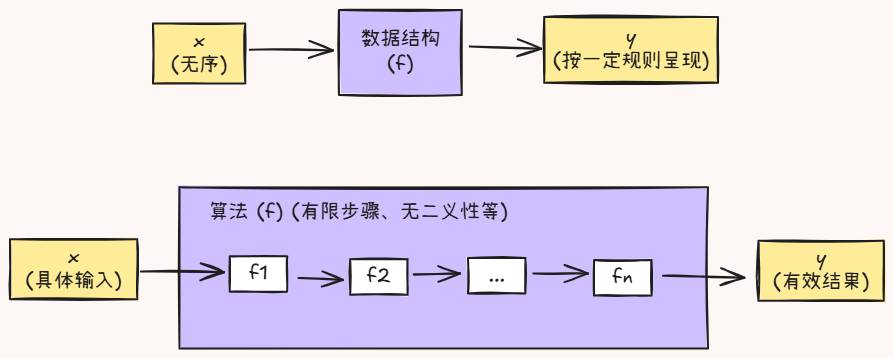
运用计算机解决一个现实问题时,一般都需要对问题建立数学模型,将其抽象成一个函数 y = f(x), 这种抽象方法掩盖了输入集合x的复杂度,当问题越复杂时,x规模会越来越庞大,x内部的元素越混乱无序,函数f处理的难度变得更大,耗费的资源更多
如何更好地整理数据,高效利用数据,建立有效关联,降低处理难度,尽可能贴近现实问题的具体现象等等,数据结构与算法在此起到作用
在数据结构与算法的介入下,为使用计算机解决现实的问题,需要对问题建立数学模型,设计该模型/系统的交互、输入输出、流程等等,提取问题的关键信息或节点,以某种形式(数据结构)组织起来,用有限的、可行的步骤(算法)模拟问题场景,最后以某种形式(数据结构)呈现出来,给出结果/得出结论/解决问题
参考书籍/网站(不限于以下列举)
- 《Data Structures and Algorithm Analysis Edition 3.2 (C++ Version)》 —— Clifford A. Shaffer
- OI Wiki
- 灵茶山艾府
概念简介
数据结构
数据的组织形式,是抽象数据类型的实现
可以直接作用在输入集合x或f内部的数据,目的是将混乱无序的整理成按某种规则约束呈现的数据
抽象数据类型(Abstract Data Type, ADT)
描述数据类型具有的某些特征功能,对外提供可操作该数据类型的接口
作为一个概念,其隐藏了具体实现
与数据结构的关系上,可以这样看:
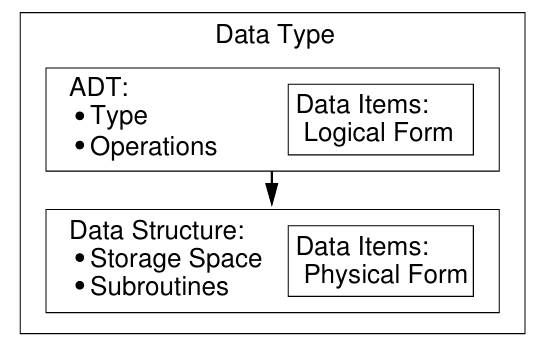
- 类型(Type):值(Value) 的集合
- 数据类型(Data Type): 一种类型,附加了一个处理该类型的操作集合
算法
解决问题的一组操作/指令(一般是数学操作/方法)
- 有限性(Finiteness): 一个算法在有限步内完成
- 确定性(Definiteness): 每一步操作都是具体确定的,无二义性; 执行算法时,相同的输入会得到相同的输出
- 可行性(Effectiveness): 算法给出的结果是正确/符合预期的,可以被拆分成基础的、可终止的步骤
- 输入(Input): 一个算法有一组具体输入
- 输出(Output): 一个算法会给出一组可解决问题的输出
复杂度分析
参考资料: 复杂度简介 OI Wiki
- 衡量一个算法效率的重要标准
- 一般而言,算法性能评估首要考虑的是算法本身在处理特定输入数量时需要的基本操作(Basic Operation)数量/次数
- 基本操作(Basic Operation): 不依赖特定值的操作。例:加法、减法等(求一个数组总和不是,依赖数组元素数量)
- 衡量算法的性能同时需要考虑数据规模,一般来说,数据规模越大,算法消耗的资源也越多,主要在 时间 和 空间 两个层面进行讨论
- 主要采用 渐进分析 来分析时间和空间随数据规模增长时的趋势,以此评估算法的性能
- 当规模增长时,通过分析变化趋势,更能区分、检测算法可处理的数据规模上限
渐进分析
描述一个函数在输入值趋近于无穷大时的行为
- 渐进符号
- (描述函数的渐进上界和渐进下界): 对于函数 和 , 当且仅当 , 使得
- (描述函数的渐进上界): 对于函数 和 , 当且仅当 , 使得
- (描述函数的渐进下界): 对于函数 和 , 当且仅当 , 使得
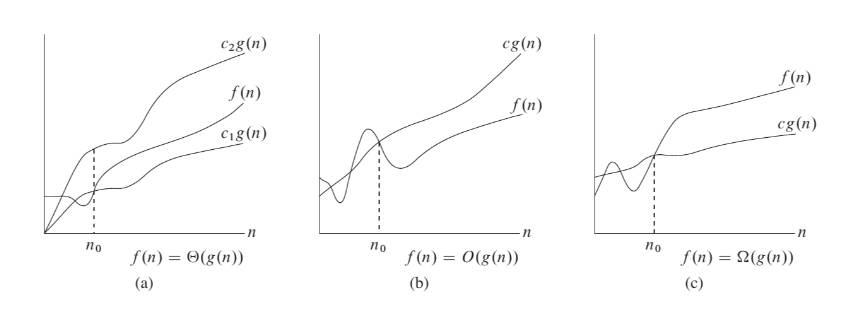
- 此外, 和 还有对应的小写符号 和 , 表示非渐进界,在此不展开
- 一般来说,探索算法可处理的规模上限,即探索函数的渐进上界,所以一般用 表示复杂度即可
内容划分
- 在接下来的笔记中,大致方向是根据在大学上课的内容来展示简单的数据结构和师傅,然后将根据自身的刷题方向罗列算法(本笔记就是为了刷题而建的),刷题内容参考 灵茶山艾府 的题单 分享|如何科学刷题?
函数模型
目录
待补充
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Forgotten Area!