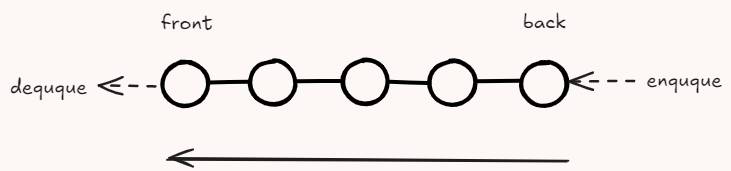
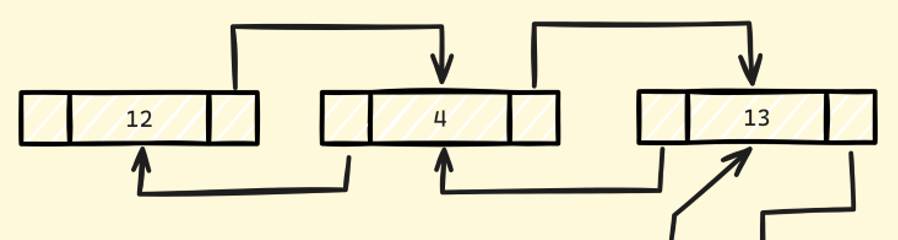
概述

栈(stack): 一种类似列表的数据结构，只能从一端访问、操作元素

简单图示

栈

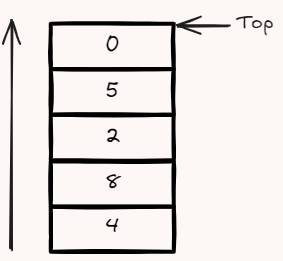
特性

  • 可操作的一端一般称为 栈顶(top), 有个访问/操作栈顶的指针，数据从栈顶加入(push)、删除(pop)，遵循 后进先出(Last In First Out, LIFO) 规则
  • 相比普通链表/列表灵活度差，但结构简单且高效

实现(C++)

ADT

1
2
3
4
5
6
7
8
9
class Stack {
public:
    Stack() {}
    virtual ~Stack() {}
    virtual void push(int data) = 0;
    virtual void pop() = 0;
    virtual int top() = 0;
    virtual int size() { return 0; }
};

链表实现

可能天然会想到这种结构
链表栈

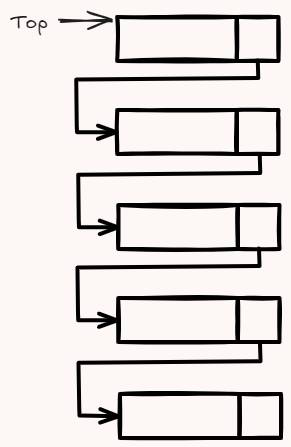
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
struct Node {
    int data;
    Node* next;

    Node(int dat, Node* nxt = nullptr) : data(dat), next(nxt) {}
};

class ListStack : public Stack {
public:
    ListStack() : Stack() {}
    virtual ~ListStack() {
        while (ptrTop) {
            // Node* tmpNode = ptrTop;
            // ptrTop = tmpNode->next();
            // delete tmpNode;
            // cnt--;
            pop();
        }
    }

    virtual void push(int data) override {
        Node* node = new Node(data);
        if (ptrTop == nullptr) ptrTop = node;
        else {
            node->next = ptrTop;
            ptrTop = node;
        }
        cnt++;
    }
    virtual void pop() override {
        if (ptrTop == nullptr) return;
        Node* tmpNode = ptrTop;
        ptrTop = tmpNode->next;
        delete tmpNode;
        cnt--;
    }
    virtual int top() override {
        if (ptrTop) {
            return ptrTop->data;
        }
        return -1;
    }
    virtual int size() override {
        return cnt;
    }
private:
    Node* ptrTop = nullptr;
    int cnt = 0;
};

数组实现

数组实现的话，给出一个 index 表示栈顶，这个 index 同时计算栈的大小，数组实现的栈可以规定栈的最大容量(其实链表也可以啦)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class ArrayStack : public Stack {
public:
    ArrayStack() : Stack() {
        memset(datas, 0, sizeof(datas)); // 可要可不要
    }
    virtual ~ArrayStack() {
        memset(datas, 0, sizeof(datas)); // 可要可不要
        topIndex = -1;
    }
    virtual void push(int data) override {
        if (topIndex < MAX_SIZE - 1) {
            datas[++topIndex] = data;
        }
    }
    virtual void pop() override {
        if (topIndex < 0) return;
        datas[topIndex] = 0; // 可要可不要
        topIndex--;
    }
    virtual int top() override {
        if (topIndex >= 0) return datas[topIndex];
        return -1;
    }
    virtual int size() override {
        return topIndex + 1;
    }

private:
    static const int MAX_SIZE = 100;
    int datas[MAX_SIZE] = {0};
    int topIndex = -1;
};

发散/随想/自身理解(?)

  • C++ 中调用 std::stack<>
  • 简单的数据结构，能下意识想到的用途就是匹配，例如字符串中 ‘{’ 匹配 ‘}’
  • 能与其它算法结合打组合拳
  • 计算机组成原理 和 操作系统 有介绍内存分配中的栈部分
  • 在本人大学学习中，栈这个数据结构在 编译原理 的语法分析中得到应用(实践)
  • 递归函数 也是 LIFO，函数本身一般也是存储在栈里的